Coupleur de Bruene vs Tandem Match
Calcul, dimensionnement, réalisations, mesures
Le coupleur directionnel fait partie de tout
système d'émission, il permet de contrôler la bonne adaptation de l'émetteur à
sa charge.
Il existe trois types de coupleurs, les coupleurs à lignes, le coupleur de
Bruene (du nom de son concepteur) et ses nombreuses variantes et le coupleur
connu sous le nom de Tandem Match.
Dans cette note, nous ne considèrerons que ces deux derniers qui sont large
bande contrairement au coupleur à lignes surtout utilisé en VHF/UHF.
Pour une analyse détaillée du fonctionnement de ces coupleurs, se reporter aux
nombreuses descriptions disponibles sur internet, notamment le site de K6JCA.
Nous nous bornerons à une étude simplifiée mais suffisante pour le
dimensionnement de ces dispositifs.
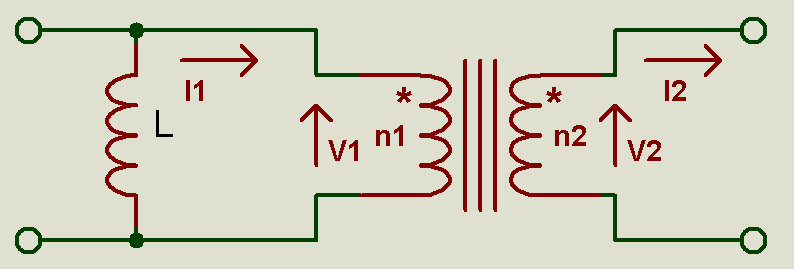
Tous les composants sont supposés parfaits, les transformateurs seront modélisés
comme un transformateur parfait en parallèle avec une inductance L.

Rappelons les équations du transformateur
parfait : n1I1 = n2I2 et V2/V1 = n2/n1
N=n2/n1
Les points marquent le début des enroulements supposés bobinés dans le même
sens. L'impédance à la fréquence F de l'inductance L est ZL=2πFL.
Coupleur de Bruene
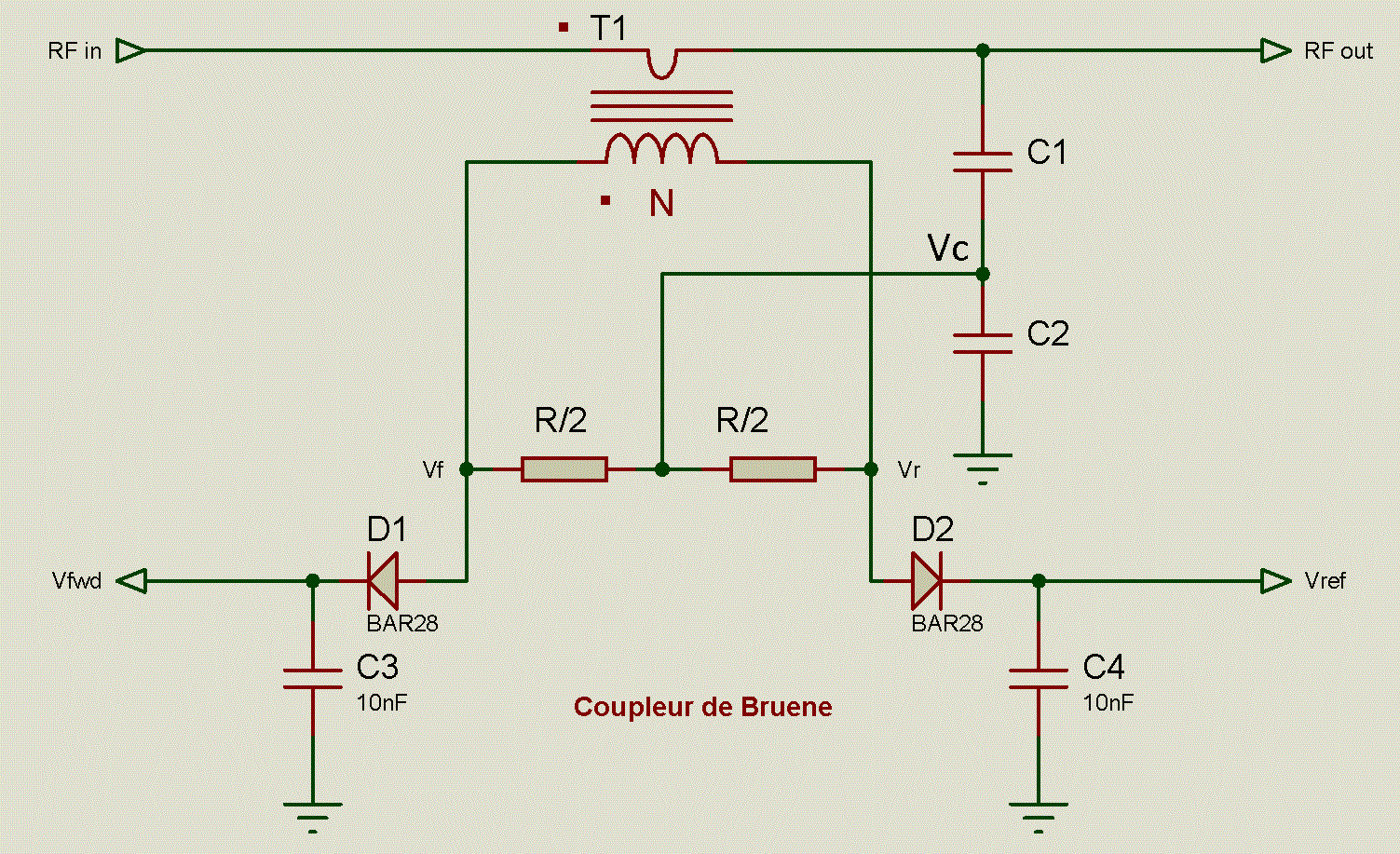
Le schéma de principe est indiqué sur la figure
suivante.
Le transformateur T1 est bobiné sur un tore en
ferrite, le primaire ne comporte qu'une seule spire (un fil traversant le tore)
et le secondaire N spires.
On suppose que la source et la charge sont adaptées d'impédance Z0 et donc que le
ROS (VSWR) est égal à 1.
La puissance P transmise à la
charge Z0 s'écrit P = U² / Z0 ou P = U² / 50
si Z0 = 50Ω ou encore P
= Z0 I²
soit I =
![]() = U / Z0
= U / Z0
Les condensateurs C1 et C2 constituent un
diviseur de tension capacitif, on montre que si C1 << C2 Vc
= U C1 / C2
Dans ces conditions la tension Vc au point milieu des condensateurs C1 et C2 est
indépendante de la fréquence.
Soit Is = I / N le courant
circulant au secondaire de T1.
En considérant qu’il n’y a pas de courant dans les diodes D1 et D2 (Haute
impédance sur les sorties Vfwd et Vref) une application de la loi d’Ohm aux
bornes des résistances R/2 donne :
Vfwd = Vc + Is R/2 et Vref = Vc - Is R/2
En remplaçant Vc et Is par leur valeur, il vient :
Vfwd = U C1/C2 + I R/2N et Vref = U C1/C2 - I R/2N
Vfwd = U (C1/C2 + R/2NZ0) Vref = U (C1/C2 - R/2NZ0)
Si on impose la condition k = C1 / C2 = R / 2NZ0 (1) sans oublier que C1 << C2 (2)
On a Vfwd = 2k U = 2(C1/C2)
Si = 50Ω et si la mesure de Vfwd s’effectue à haute impédance, la capacité C3 se charge à la tension crête de la sinusoïde et on a
Vfwd crête = 20 (C1/C2) √P ce qui permet une mesure précise de la puissance directe indépendamment de la fréquence.
Dans le cas général, le ROS n'est pas égal à 1 et on a:
Vfwd crête = 20 (C1/C2) √Pfwd et Vref crête = 20 (C1/C2) √Pref
NB: Vfwd crête et Vref crête sont des tensions continues égales à la tension crête de la sinusoïde c'est à dire √2 fois la tension efficace.
Dimensionnement des composants
A partir de l’équation (1) on peut déterminer les valeurs de k, N et R. Etant donné que nous avons une équation à trois inconnues, il faut choisir 2 valeurs et calculer la troisième.
Calcul de R
On choisit k et N d’où R = 2NZ0 C1/C2
Calcul de N
On choisit k et R d’où N = (R/2Z0)(C1/C2)
Calcul de C1 et C2
On fixe C1 et C2 = C1/k ou si on a choisi N et R C2 = 2NZ0C1/R
Contraintes à respecter
· - C1 << C2 Pour que le diviseur capacitif soit indépendant de la fréquence.
· -
A
la fréquence de travail la plus basse l’impédance du secondaire de T1 doit être
grande devant R, on prendra 2πFL/R
>10.
Ceci entraine une contrainte supplémentaire sur le nombre de
spires N et sur le choix du tore.
- - - Choix du tore en ferrite
Pour dimensionner correctement le transformateur il faut connaitre les dimensions
du tore, sa section effective Ae et son
inductance spécifique Al.
On calcule ensuite l’inductance L= Al N² et son impédance Z=2πFL à la fréquence
la plus basse.
On vérifie ainsi que le nombre spires N convient pour satisfaire le critère
précédent.
· - Les
pertes dans le tore en ferrite augmentant comme le carré de la fréquence, Amidon
conseille de limiter l’induction B à une valeur que l’on peut approximer par la
formule empirique : Bmax = 150 /√F avec B en gauss et F en MHz.
Il faut calculer l’induction à l’aide de la formule classique Bmax =
10⁴ Vcrête/(4,44FNAe)
avec B en Gauss, F en MHz, Ae en mm²
Pour cela on remplace V par Rp I où I est le courant primaire i = √(P/Z0) et Rp la résistance R vue du primaire Rp = R/N²
· -
L’impédance de C1 à la fréquence la
plus haute doit être grande devant Z0 afin de ne pas perturber le
fonctionnement :
1/2πFmax C1 >> Z0
Ne pas oublier que C1 voit la tension crête aux bornes de la charge...
· - Les mesures de Vfwd et Vref doivent être effectuées à haute impédance, les condensateurs se chargeant à la tension crête.
Tous ces calculs peuvent être aisément réalisés par une feuille de calcul Excel
Exemple de dimensionnement
On veut réaliser un coupleur
fonctionnant entre 7 et 50MHz, pour une puissance nominale de 100W.
Le tore disponible fait 14x9x5 mm en matériau 4C65 (violet). Sa section
effective est de 12,3 mm² et son inductance spécifique Al est de 55.
Après quelques itérations dans la feuille de calcul, on choisit d'utiliser deux
résistance de 27Ω pour R/2 (soit R= 54Ω) , un bobinage de 18 spires et une
capacité C1 de 3pF (en fait un condensateur ajustable de 6pF).
Le calcul donne une valeur de C2=100pF, une induction maximale de 0,05 gauss,
une inductance L du secondaire de 18µH. Tous les critères précédents étant
satisfaits, il n'y a plus qu'à passer à la réalisation. Nous utiliserons une
variante du coupleur de Bruene dont le schéma est le suivant
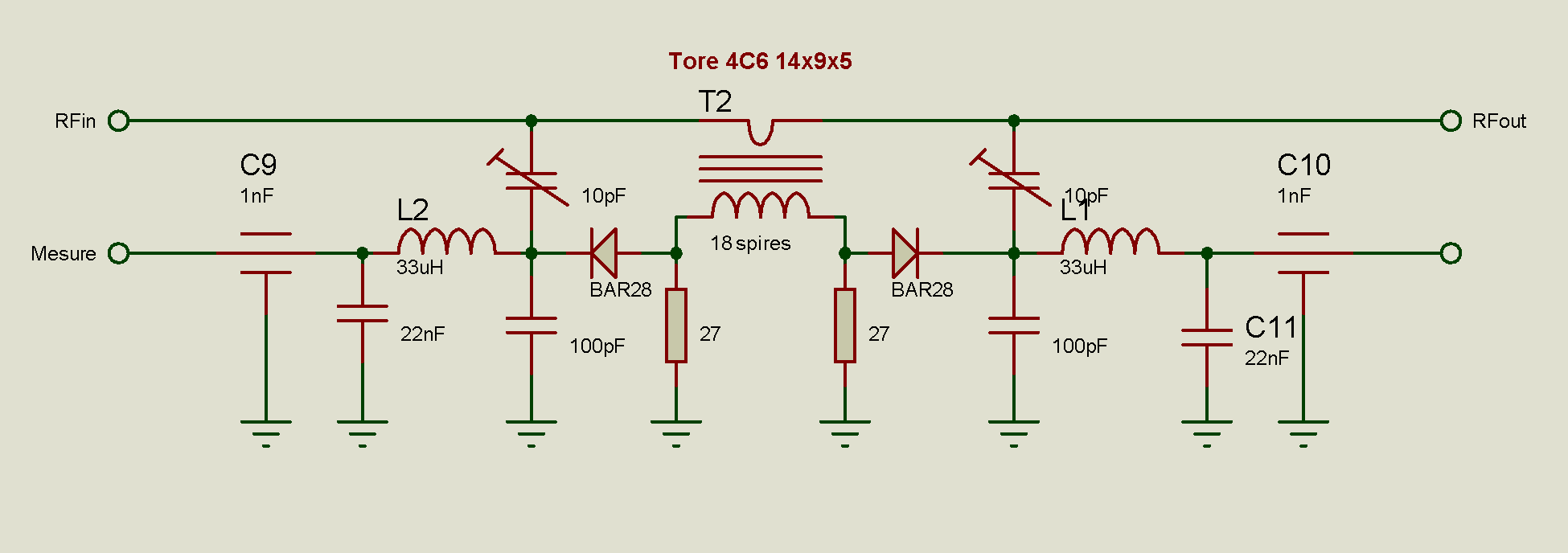
Le circuit est monté en l'air dans un petit boitier en fer blanc équipé de deux prises SO239. Les deux prises sont reliées par un morceau de câble coaxial qui traverse le tore et dont la tresse est reliée à la masse d'un seul côté, celle ci ne servant que d'écran. Les deux résistances de 27Ω doivent être parfaitement appariées ainsi que les deux condensateurs de 100pF

Le réglage s'effectue sur charge 50Ω
à puissance nominale. Ajuster le condensateur ajustable pour le minimum de
tension sur la sortie Vref, puis retourner le coupleur et régler l'autre
condensateur pour obtenir le minimum de tension sur la sortie Vfwd. Les tensions
Vref et Vfwd doivent être mesurées avec un voltmètre numérique haute impédance.
Refaire la manip une ou deux fois jusqu'à obtenir un minimum de tension Vref.
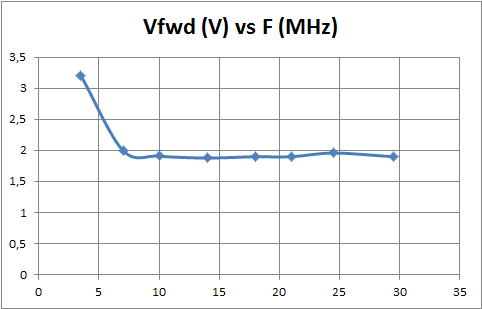
La courbe ci dessous montre la tension directe Vfwd relevée en fonction de la puissance sur charge 50Ω à 21MHz, on peut constater qu'on est très proche de la valeur théorique Vfwd=0,6√P.
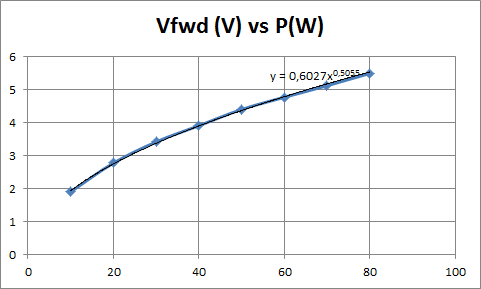
La bande passante est conforme à la théorie comme le montre la courbe suivante, relevée à P=10W sur charge 50Ω. On constate que la précision est mauvaise à basse fréquence, ce qui est normal car le matériau 4C65 est adapté aux fréquences élevées et possède un Al de seulement 55, ce qui ne permet pas de satisfaire le critère de 2πFL/R >10 au dessous de 7 MHz. Pour élargir la bande passante vers les basses fréquences, il faudrait choisir un matériau de plus forte perméabilité ou accoler deux tores.
Parmi les contraintes à respecter, il y a la mesure à haute impédance des tensions Vfwd et Vref . Beaucoup de réalisations utilisent un simple galvanomètre pour mesurer ces tensions, cela fonctionne mais la tension mesurée n'est plus la valeur crête redressée mais une valeur moyenne qui dépend de la résistance du circuit, on perd donc en reproductibilité. Je préconise donc d'utiliser un ampli opérationnel monté en suiveur. Cet ampli doit pouvoir mesurer des tensions proches du zéro. Un LM358 fera parfaitement l'affaire (ne pas utiliser d'ampli à JFET comme le TL082), alimenté en mono tension entre 10 et 24V.
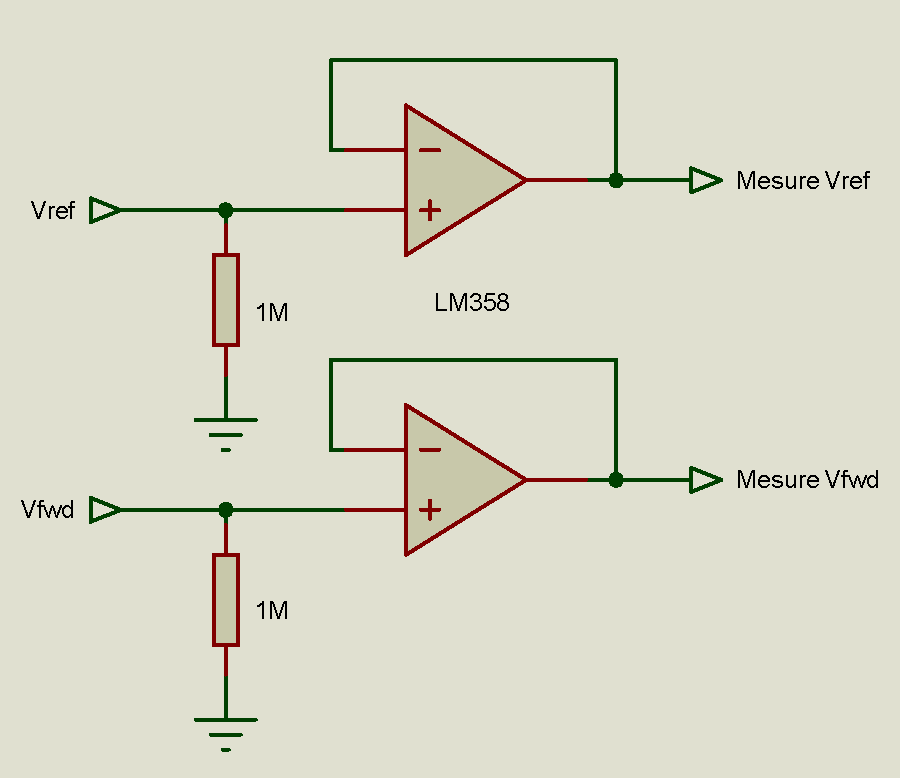
Les tensions ainsi disponibles peuvent alimenter un galvanomètre, un bargarph comme le LM3914 ou encore un circuit de protection contre l'excès de ROS.
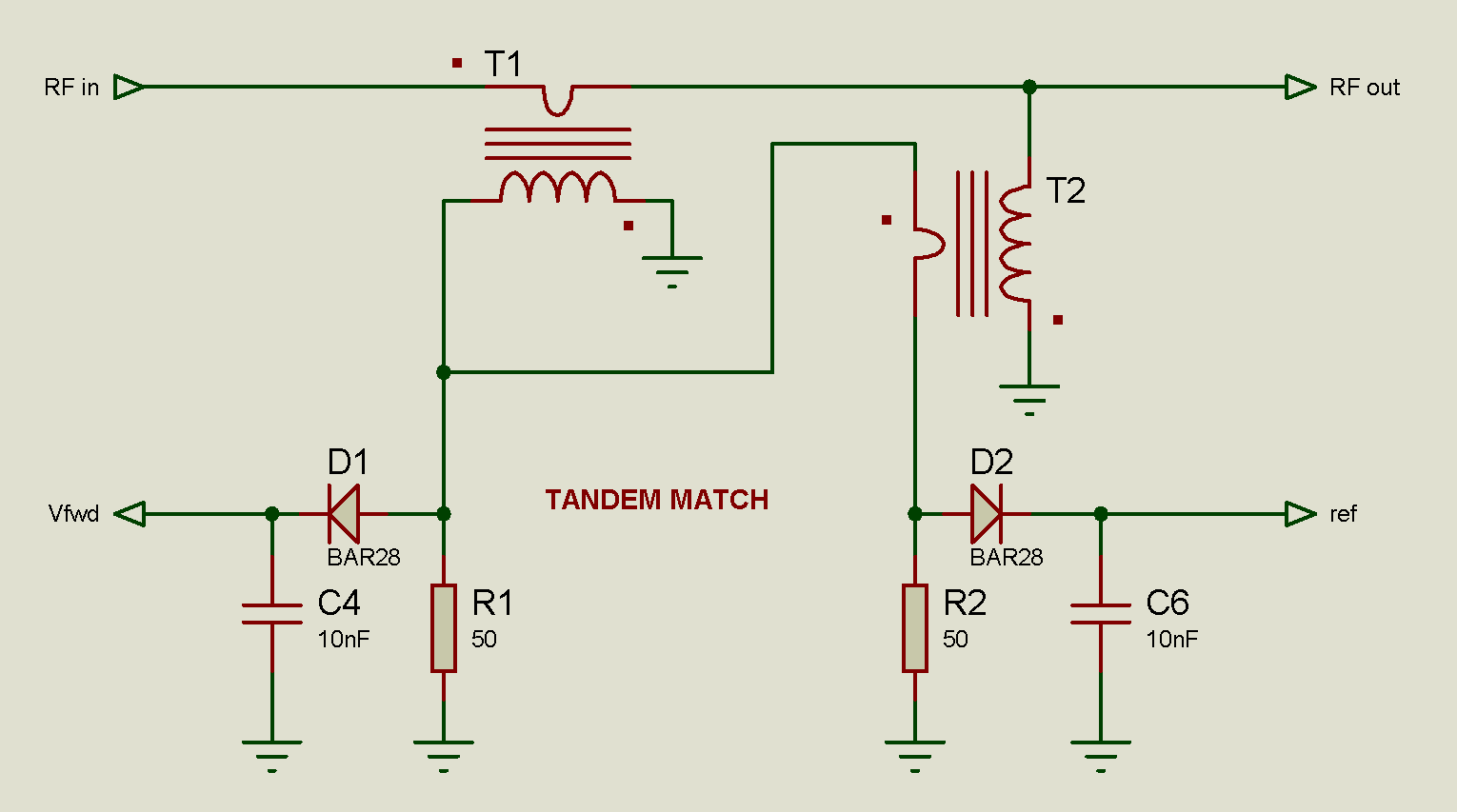
Coupleur Tandem Match
Ce coupleur est
moins connu que le coupleur de Bruene, mais tout aussi intéressant. Alors que le
premier utilise un diviseur capacitif pour mesurer la tension, le Tandem match
fait appel à un transformateur.
Les deux transformateurs T1 et T2 doivent avoir le même rapport de
transformation N et les résistances R1 et R2 doivent être égales à Z0, c'est à
dire 50Ω.
Les sorties Vfwd et Vref doivent être reliées à une impédance élevé de manière à
ce que l'on puisse négliger le courant traversant les diodes D1 et D2.
Tout comme
précédemment, nous allons faire une analyse simplifiée en supposant que tous les
éléments sont parfaits, que le ROS est égal à 1 et que l'impédance du système Z0
est 50Ω.
La puissance P transmise à la
charge Z0 s'écrit P = U² / Z0 ou P = U² / 50
si Z0 = 50Ω ou encore
P = Z0 I²
soit I =
![]() = U / Z0
= U / Z0
On en déduit que la tension crête aux bornes de la charge est (le signal étant supposé sinusoïdal)
Uc=√2√(P Z0) = 10√P et que le courant crête dans la charge est Ic=√2 √(P/Z0)
La résistance R1 est traversée par deux courants provenant de T1 et T2. En appliquant le principe de superposition on établit l'équation de la tension crête Vfwd (puisqu'il n'y a pas de courant consommé sur la sortie Vfwd, la capacité se charge à la tension crête de la sinusoïde).
Vfwd = 10√P/N où N est le nombre de spires du transformateur (1 spire au primaire pour T1 et 1 spire au secondaire pour T2)
On effectue le même calcul en sens inverse et on obtient Vref = 10√P/N
En résumé nous aurons donc
Vfwd = 10√Pfwd/N et Vref = 10√Pref/N
Ce qui permet une mesure des puissances directe et réfléchie indépendamment de la fréquence
Dimensionnement
La plus grosse difficulté
réside dans le calcul des transformateurs notamment T2.
Les deux transformateurs T1
et T2 doivent avoir le même rapport de transformation N (1 spire d’un côté et N
spires de l’autre), mais les contraintes sont différentes.
T1 est un
transformateur de courant et ne pose pas de problème. En revanche le primaire de
T2 est soumis à la pleine tension RF, par exemple pour 100W dans 50Ω, la tension
crête est de 100V. Ceci entraine deux contraintes :
- L’inductance L du primaire de T2 doit être suffisante pour que son impédance
Z=2πFL soit grande devant 50Ω à la fréquence de fonctionnement la plus basse.
- Les pertes dans le tore en ferrite augmentant comme le carré de la fréquence,
il est conseillé de limiter l’induction B à une valeur que l’on peut approximer
par la formule empirique :
Bmax = 150 /√F avec B en gauss et F en MHz
Ceci conditionne le choix du tore et le nombre de spires N
Pour dimensionner
correctement le transformateur il faut connaitre les dimensions du tore, sa section effective Ae
et son inductance spécifique Al
On calcule ensuite l’inductance L= Al N² et son impédance Z=2πFL à la fréquence
la plus basse.
On détermine ainsi le nombre spires N qui convient pour satisfaire le premier
critère.
Il faut maintenant vérifier le critère d’induction maximale à l’aide de la formule :
Bmax = 10⁴ Vcrête/(4,44FNAe) avec B en Gauss, F en MHz, Ae en mm²
Si la condition n’est pas satisfaite, il faut prendre un tore plus gros ou accoler plusieurs tores. Choisir de préférence un (ou plusieurs) tore(s) avec un diamètre intérieur pas trop grand afin d’assurer un bon couplage primaire-secondaire.
Cas du transformateur T1
Le calcul de l’induction s’effectue de la même manière en remplaçant V par Rp I où I est le courant primaire I=√(P/Z0) et Rp la résistance vue du primaire Rp=50/N²
Bmax = 10⁴ Icrête Rp/(4,44FNAe)
En général, l’induction dans le transformateur T1 est très inférieure à celle de T2, ce qui permet d’utiliser un tore plus petit.
Nous allons reprendre l'exemple précédent, à
savoir fréquence 7 à 50 MHz, Puissance au moins 100W en utilisant les mêmes
tores 14x9x5 mm en matériau 4C65.
Un premier calcul avec excel montre qu'avec un
seul tore on est limite en induction pour T2. J'en ai donc accolé deux ce qui me
donne une section effective de 24,6mm² et un Al de 110. Avec 20 spires le calcul
donne une tension Vfwd de 5V et une inductance primaire de T2 de 44µH. Il ne
reste plus qu'à construire.

Le circuit est monté sur un morceau d'époxy gravé au cutter. Les deux résistances de 50Ω sont réalisées par la mise en parallèle de deux résistances de 100Ω appariées de manière à obtenir 50Ω précisément. Le primaire de T1 et le secondaire de T2 sont réalisés à l'aide d'un morceau de cable coaxial dont la tresse est reliée à la masse d'un seul coté.
Note importante: Il est impératif de placer une cloison de blindage entre les deux transformateurs
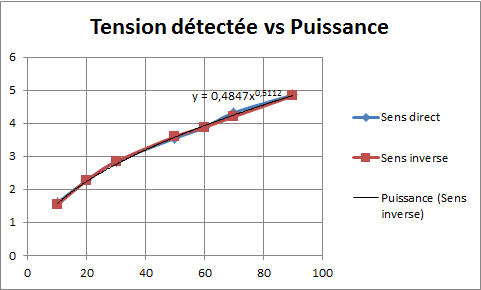
La courbe
ci-dessus montre que la tension détectée est très proche de la théorie qui
indique Vfwd= 0,5√P
La bande passante est conforme au calcul avec une divergence aux basses
fréquences comme indiqué précédemment.
Les résultats étant tout à fait encourageants, j'ai réalisé une seconde version, plus compacte destinée à intégrer un ampli à LDMOS pour suivre un FT817

Vous pouvez télécharger ma feuille de calcul ici
Dernière mise à jour le 4 mai 2022
73 Joël F6CSX